SHA-256 的原理与实现 | Mogeko`s Blog
SHA-2(Secure Hash Algorithms 2)是一系列散列函数算法标准,可以说是目前最重要,使用最广泛的 Hash 函数家族。SHA-256 和 SHA-512 又是家族中最流行的两支。在量子计算机真正实用化之前,它都是密码学中的重要武器。
今天,就来研究一下 SHA-256 的算法原理,并试着用 JavaScript 实现了一下。
💡
Hash 函数可以用来保护密码,但 Hash 函数不是用来加密的! Hash 函数是用来「描述」数据特征的,是单向的(不能从 Hash 值中「解密」回明文),而任何一种加密算法都是双向的(明文 -> 密文,密文 -> 明文)。
SHA-256 的核心原理可以用一句话来概括: 通过一系列复杂的数学计算,将任意长度的输入数据转换成一个固定长度(256 位)的「数字指纹」 。核心目标是确保这个「数字指纹」的 唯一性 、 不可逆性 和 抗碰撞性 。
SHA-256 对消息做 Hash 摘要,例如:
The quick brown fox jumps over the lazy dog. 经过 SHA-256 算法处理后将会变成:
ef537f25c895bfa782526529a9b63d97aa631564d5d789c2b765448c8635fb6c 以下是 SHA-256 算法处理数据的 核心步骤 :
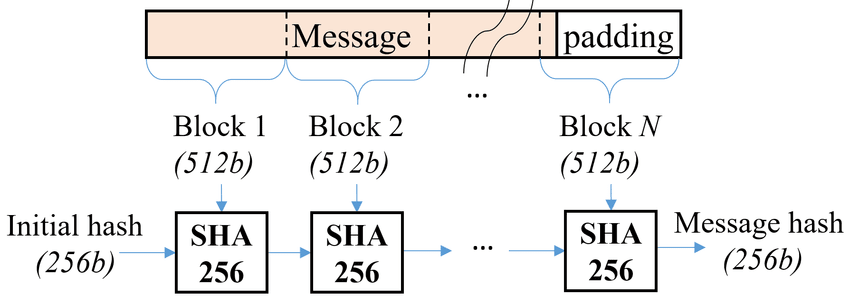
数据填充 : 将目标数据长度调整为 512 比特的整数倍数。
分块处理 : 将填充后的数据分割成多个 512 比特的块 ,每个块单独处理。
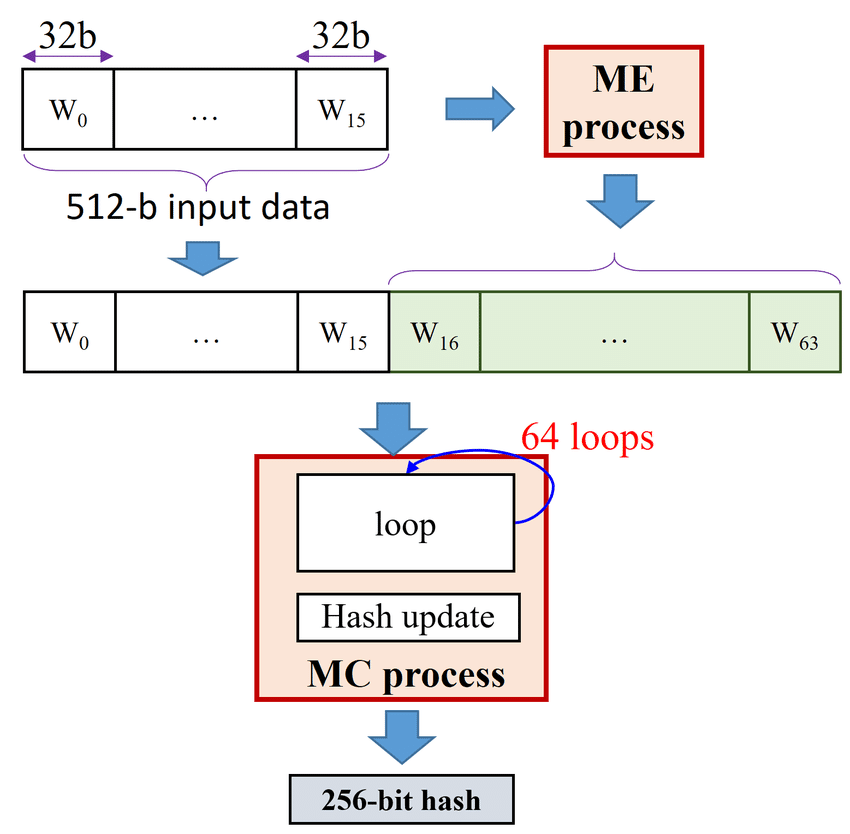
消息扩展: 将每个 512 比特的块(16 个 32 比特的字)扩展为 64 个 32 比特的字 。
迭代压缩: 将 64 个 32 比特的字经过 64 轮复杂运算 ,最终变为一个 256 比特的块。
更新 Hash 值: 每处理完一个块,我们都会将当前块的结果与 初始 Hash 值 (或前一块的结果) 按位相加 ,形成新的中间 Hash 值。
最终输出: 所有的块处理完毕后,将 8 个中间 Hash 值(每个 32 位, 8 ∗ 32 = 256 8 * 32 = 256 8 ∗ 32 = 256 bit) 拼接 成一个 256 位的二进制字符串;为了方便阅读,我们通常会将其转换为一个 64 位十六进制的字符串。
其中的核心数学原理主要是 混淆 与 扩散 (Confusion & Diffusion):
扩散: 让输入的微小变动扩散到整个 Hash 值(如改动 1 bit,最终结果 50% 的 bit 都会改变)
混淆: 通过位运算和轮函数,让输入和输出之间的关系变得及其复杂。
前文提到了 SHA-256 算法中会用到 8 个 Hash 初始值( H i H_i H i );他们分别是:
H 0 = 6 a 09 e 667 H 1 = b b 67 a e 85 H 2 = 3 c 6 e f 372 H 3 = a 54 f f 53 a H 4 = 510 e 527 f H 5 = 9 b 05688 c H 6 = 1 f 83 d 9 a b H 7 = 5 b e 0 c d 19 \begin{aligned} H_0 &= 6a09e667 \\ H_1 &= bb67ae85 \\ H_2 &= 3c6ef372 \\ H_3 &= a54ff53a \\ H_4 &= 510e527f \\ H_5 &= 9b05688c \\ H_6 &= 1f83d9ab \\ H_7 &= 5be0cd19\end{aligned} H 0 H 1 H 2 H 3 H 4 H 5 H 6 H 7 = 6 a 09 e 667 = bb 67 a e 85 = 3 c 6 e f 372 = a 54 ff 53 a = 510 e 527 f = 9 b 05688 c = 1 f 83 d 9 ab = 5 b e 0 c d 19
H 1 H_1 H 1 至 H 7 H_7 H 7 来自于自然数中前 8 个质数( 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 2, 3, 5, 7, 11, 13, 17, 19 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 )的 平方根 的小数部分的前 32 位。
除此之外,还会用到 64 个 Hash 常量( K t K_{t} K t ),他们分别是:
428 a 2 f 98 71374491 b 5 c 0 f b c f e 9 b 5 d b a 5 3956 c 25 b 59 f 111 f 1 923 f 82 a 4 a b 1 c 5 e d 5 d 807 a a 98 12835 b 01 243185 b e 550 c 7 d c 3 72 b e 5 d 74 80 d e b 1 f e 9 b d c 06 a 7 c 19 b f 174 e 49 b 69 c 1 e f b e 4786 0 f c 19 d c 6 240 c a 1 c c 2 d e 92 c 6 f 4 a 7484 a a 5 c b 0 a 9 d c 76 f 988 d a 983 e 5152 a 831 c 66 d b 00327 c 8 b f 597 f c 7 c 6 e 00 b f 3 d 5 a 79147 06 c a 6351 14292967 27 b 70 a 85 2 e 1 b 2138 4 d 2 c 6 d f c 53380 d 13 650 a 7354 766 a 0 a b b 81 c 2 c 92 e 92722 c 85 a 2 b f e 8 a 1 a 81 a 664 b c 24 b 8 b 70 c 76 c 51 a 3 d 192 e 819 d 6990624 f 40 e 3585 106 a a 070 19 a 4 c 116 1 e 376 c 08 2748774 c 34 b 0 b c b 5 391 c 0 c b 3 4 e d 8 a a 4 a 5 b 9 c c a 4 f 682 e 6 f f 3 748 f 82 e e 78 a 5636 f 84 c 87814 8 c c 70208 90 b e f f f a a 4506 c e b b e f 9 a 3 f 7 c 67178 f 2 \begin{aligned} 428a2f98 &\space 71374491 & b5c0fbcf &\space e9b5dba5 & 3956c25b &\space 59f111f1 & 923f82a4 &\space ab1c5ed5 \\ d807aa98 &\space 12835b01 & 243185be &\space 550c7dc3 & 72be5d74 &\space 80deb1fe & 9bdc06a7 &\space c19bf174 \\ e49b69c1 &\space efbe4786 & 0fc19dc6 &\space 240ca1cc & 2de92c6f &\space 4a7484aa & 5cb0a9dc &\space 76f988da \\ 983e5152 &\space a831c66d & b00327c8 &\space bf597fc7 & c6e00bf3 &\space d5a79147 & 06ca6351 &\space 14292967 \\ 27b70a85 &\space 2e1b2138 & 4d2c6dfc &\space 53380d13 & 650a7354 &\space 766a0abb & 81c2c92e &\space 92722c85 \\ a2bfe8a1 &\space a81a664b & c24b8b70 &\space c76c51a3 & d192e819 &\space d6990624 & f40e3585 &\space 106aa070 \\ 19a4c116 &\space 1e376c08 & 2748774c &\space 34b0bcb5 & 391c0cb3 &\space 4ed8aa4a & 5b9cca4f &\space 682e6ff3 \\ 748f82ee &\space 78a5636f & 84c87814 &\space 8cc70208 & 90befffa &\space a4506ceb & bef9a3f7 &\space c67178f2\end{aligned} 428 a 2 f 98 d 807 aa 98 e 49 b 69 c 1 983 e 5152 27 b 70 a 85 a 2 b f e 8 a 1 19 a 4 c 116 748 f 82 ee 71374491 12835 b 01 e f b e 4786 a 831 c 66 d 2 e 1 b 2138 a 81 a 664 b 1 e 376 c 08 78 a 5636 f b 5 c 0 f b c f 243185 b e 0 f c 19 d c 6 b 00327 c 8 4 d 2 c 6 df c c 24 b 8 b 70 2748774 c 84 c 87814 e 9 b 5 d ba 5 550 c 7 d c 3 240 c a 1 cc b f 597 f c 7 53380 d 13 c 76 c 51 a 3 34 b 0 b c b 5 8 cc 70208 3956 c 25 b 72 b e 5 d 74 2 d e 92 c 6 f c 6 e 00 b f 3 650 a 7354 d 192 e 819 391 c 0 c b 3 90 b e fff a 59 f 111 f 1 80 d e b 1 f e 4 a 7484 aa d 5 a 79147 766 a 0 abb d 6990624 4 e d 8 aa 4 a a 4506 ce b 923 f 82 a 4 9 b d c 06 a 7 5 c b 0 a 9 d c 06 c a 6351 81 c 2 c 92 e f 40 e 3585 5 b 9 cc a 4 f b e f 9 a 3 f 7 ab 1 c 5 e d 5 c 19 b f 174 76 f 988 d a 14292967 92722 c 85 106 aa 070 682 e 6 ff 3 c 67178 f 2
与 Hash 初始值类似,它们分别取自于自然数中前 64 个质数( 2 , 3 , 5 , … , 307 , 311 2, 3, 5, \dotsc, 307, 311 2 , 3 , 5 , … , 307 , 311 )的 立方根 的小数部分的前 32 位。
然后是对数据进行预处理,主要是两个步骤: 补位 与 分块 。
对数据进行补位处理,确保其最终的长度是 512 位的倍数。其规则为,先在末尾补上一位 1 1 1 (即 0x80 ),表示填充开始。再在末尾补上 k k k 个 0 0 0 ,直至原始数据长度 L L L 满足:
L + 1 + k ≡ 448 ( m o d 512 ) L + 1 + k \equiv 448 \pmod {512} L + 1 + k ≡ 448 ( mod 512 )
最后,在末尾附加原始数据长度 L L L 的 二进制表示 (大端序,64 位)。
例如,假设数据位 abc ,则其对应的 ASCII 码和二进制编码如下:
所以 abc 的二进制编码为:
01100001 01100010 01100011 01100001 \space 01100010 \space 01100011 01100001 01100010 01100011
先在末尾补上一位 1 1 1 :
01100001 01100010 01100011 1 01100001 \space 01100010 \space 01100011 \space 1 01100001 01100010 01100011 1
再补上 423 个 0 0 0 :
01100001 01100010 01100011 1 0 … 0 ⏟ 423 times 01100001 \space 01100010 \space 01100011 \space 1 \space \underbrace{0 \dotsc 0}_{423 \text{ times}} 01100001 01100010 01100011 1 423 times 0 … 0
最后,在末尾附加数据 abc 的长度 24 的 二进制表示 (64 位):
01100001 01100010 01100011 1 0 … 0 ⏟ 458 times 11000 ⏞ 512 bit \overbrace{01100001 \space 01100010 \space 01100011 \space 1 \space \underbrace{0 \dotsc 0}_{458 \text{ times}} 11000}^{512 \text{ bit}} 01100001 01100010 01100011 1 458 times 0 … 0 11000 512 bit
分块处理很好理解,就是将填充后的数据 M M M 分解成 n n n 个大小为 512 比特的块。
此后在做循环处理时,每次对 512 比特的数据块进行运算,得到的 256 比特的结果再与下一个块进行运算,如此运行 n n n 次后,得到最终的哈希值,即 256 bit 的「数字签名」。
终于,我们来到了最核心的运算环节!
SHA-256 算法的运算主要包括两个方面: 消息扩展 和 消息压缩 (Message Expansion & Message Compression),其中消息压缩又可以拆分为 主循环 和 更新 Hash 值 。
消息扩展和消息压缩十分符合《道德经》中的「有无相生,难易相成」的思想;先扩展,再压缩,让数据变得混沌,从而实现 不可逆性 和 抗碰撞性 ;又因为算法是完完全全没有任何副作用的纯函数,所以天生具有 唯一性 。
消息扩展的目的是将原始数据块扩展为更长的位序列,以供后续的轮函数处理。消息扩展通过引入非线性变换和复杂的数据依赖关系,增强算法的安全性和扩散性。
在 SHA-256 中,吗,每个 512 比特的数据块会被分块处理,消息扩散的目标是将这 512 比特(16 个 32 比特的字)扩展为 64 个 32 比特的字,供后续 64 轮运算(即「主循环」)使用。
初始分解: 将 512 比特的输入块分割为 16 个初始字 (每个 32 比特),记做:
扩展生成: 剩余的 48 个字( W 16 , … , W 63 W_{16}, \dotsc, W_{63} W 16 , … , W 63 )通过以下公式生成:
消息压缩负责将消息扩展生成的 64 个 32 比特的字( W t W_t W t )和 Hash 中间值 (初始化为 H i H_i H i )混合,并生成新的 Hash 状态。
以下是具体步骤:
初始化工作变量: 将初始化 Hash 值( H i H_i H i )赋值给工作变量:
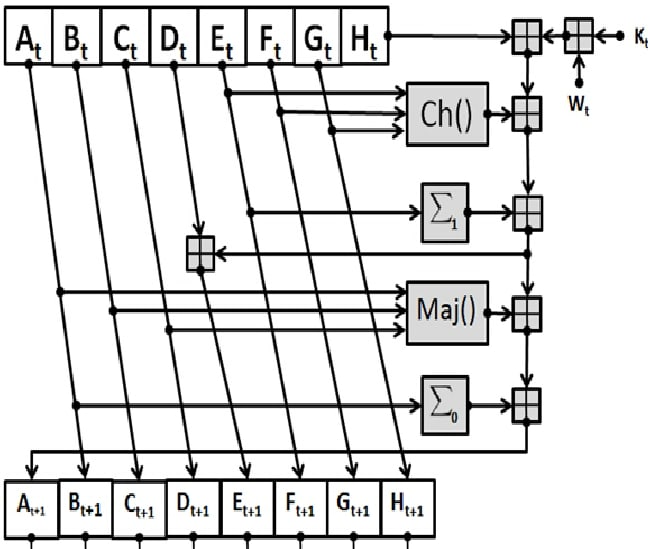
主循环(64 轮循环运算): 消息扩展生成的 64 个 32 比特的字 ( W t W_t W t )进行 64 轮迭代,每轮先计算临时变量 T 1 T_1 T 1 和 T 2 T_2 T 2 :
更新 Hash 中间值:64 轮迭代计算结束后,将工作变量与初始 Hash 值相加,然后模 2 32 2^{32} 2 32 :
function sha256 ( input : string ) : string { // 辅助函数定义 const Ch = ( x : number, y : number, z : number ) = > ( x & y ) ^ ( ~ x & z ) ; const Maj = ( x : number, y : number, z : number ) = > ( x & y ) ^ ( x & z ) ^ ( y & z ) ; const Sigma0 = ( x : number ) = > rotr ( x , 2 ) ^ rotr ( x , 13 ) ^ rotr ( x , 22 ) ; const Sigma1 = ( x : number ) = > rotr ( x , 6 ) ^ rotr ( x , 11 ) ^ rotr ( x , 25 ) ; const sigma0 = ( x : number ) = > rotr ( x , 7 ) ^ rotr ( x , 18 ) ^ ( x > > > 3 ) ; const sigma1 = ( x : number ) = > rotr ( x , 17 ) ^ rotr ( x , 19 ) ^ ( x > > > 10 ) ; const rotr = ( x : number, n : number ) = > ( ( x > > > n ) | ( x < < ( 32 - n ) ) ) > > > 0 ; // 初始化哈希值 H 和常量 K const H = new Uint32Array ( [ 0x6a09e667 , 0xbb67ae85 , 0x3c6ef372 , 0xa54ff53a , 0x510e527f , 0x9b05688c , 0x1f83d9ab , 0x5be0cd19 , ] ) ; const K = new Uint32Array ( [ 0x428a2f98 , 0x71374491 , 0xb5c0fbcf , 0xe9b5dba5 , 0x3956c25b , 0x59f111f1 , 0x923f82a4 , 0xab1c5ed5 , 0xd807aa98 , 0x12835b01 , 0x243185be , 0x550c7dc3 , 0x72be5d74 , 0x80deb1fe , 0x9bdc06a7 , 0xc19bf174 , 0xe49b69c1 , 0xefbe4786 , 0x0fc19dc6 , 0x240ca1cc , 0x2de92c6f , 0x4a7484aa , 0x5cb0a9dc , 0x76f988da , 0x983e5152 , 0xa831c66d , 0xb00327c8 , 0xbf597fc7 , 0xc6e00bf3 , 0xd5a79147 , 0x06ca6351 , 0x14292967 , 0x27b70a85 , 0x2e1b2138 , 0x4d2c6dfc , 0x53380d13 , 0x650a7354 , 0x766a0abb , 0x81c2c92e , 0x92722c85 , 0xa2bfe8a1 , 0xa81a664b , 0xc24b8b70 , 0xc76c51a3 , 0xd192e819 , 0xd6990624 , 0xf40e3585 , 0x106aa070 , 0x19a4c116 , 0x1e376c08 , 0x2748774c , 0x34b0bcb5 , 0x391c0cb3 , 0x4ed8aa4a , 0x5b9cca4f , 0x682e6ff3 , 0x748f82ee , 0x78a5636f , 0x84c87814 , 0x8cc70208 , 0x90befffa , 0xa4506ceb , 0xbef9a3f7 , 0xc67178f2 , ] ) ; // 将输入转换为字节数组 const bytes = new TextEncoder ( ) . encode ( input ) ; // 消息填充 const len = bytes . length ; const totalBits = len * 8 ; const paddingBytes = ( 64 - ( ( len + 8 + 1 ) % 64 ) ) % 64 ; const padded = new Uint8Array ( len + 1 + paddingBytes + 8 ) ; padded . set ( bytes ) ; padded [ len ] = 0x80 ; // 添加 1 的位 // 添加消息长度(64 位大端) const view = new DataView ( padded . buffer ) ; view . setUint32 ( padded . length - 8 , Math . floor ( totalBits / 0x100000000 ) , false , ) ; view . setUint32 ( padded . length - 4 , totalBits > > > 0 , false ) ; // 处理每个 512 位块 for ( let i = 0 ; i < padded . length ; i += 64 ) { const chunk = padded . subarray ( i , i + 64 ) ; const w = new Uint32Array ( 64 ) ; // 将块分解为 16 个 32 位大端字 for ( let j = 0 ; j < 16 ; j ++ ) { w [ j ] = ( ( chunk [ j * 4 ] < < 24 ) | ( chunk [ j * 4 + 1 ] < < 16 ) | ( chunk [ j * 4 + 2 ] < < 8 ) | chunk [ j * 4 + 3 ] ) > > > 0 ; } // 扩展消息块 for ( let j = 16 ; j < 64 ; j ++ ) { w [ j ] = ( w [ j - 16 ] + sigma0 ( w [ j - 15 ] ) + w [ j - 7 ] + sigma1 ( w [ j - 2 ] ) ) > > > 0 ; } // 初始化工作变量 let [ a , b , c , d , e , f , g , h ] = H ; // 主循环处理 for ( let j = 0 ; j < 64 ; j ++ ) { const temp1 = ( h + Sigma1 ( e ) + Ch ( e , f , g ) + K [ j ] + w [ j ] ) > > > 0 ; const temp2 = ( Sigma0 ( a ) + Maj ( a , b , c ) ) > > > 0 ; h = g ; g = f ; f = e ; e = ( d + temp1 ) > > > 0 ; d = c ; c = b ; b = a ; a = ( temp1 + temp2 ) > > > 0 ; } // 更新哈希值 H [ 0 ] = ( H [ 0 ] + a ) > > > 0 ; H [ 1 ] = ( H [ 1 ] + b ) > > > 0 ; H [ 2 ] = ( H [ 2 ] + c ) > > > 0 ; H [ 3 ] = ( H [ 3 ] + d ) > > > 0 ; H [ 4 ] = ( H [ 4 ] + e ) > > > 0 ; H [ 5 ] = ( H [ 5 ] + f ) > > > 0 ; H [ 6 ] = ( H [ 6 ] + g ) > > > 0 ; H [ 7 ] = ( H [ 7 ] + h ) > > > 0 ; } // 生成十六进制哈希字符串 return Array . from ( H , ( n ) = > n . toString ( 16 ) . padStart ( 8 , "0" ) ) . join ( "" ) ; } // 示例用法 console . log ( sha256 ( "" ) ) ; // e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855 console . log ( sha256 ( "abc" ) ) ; // ba7816bf8f01cfea414140de5dae2223b00361a396177a9cb410ff61f20015ad 字符 ASCII 码 二进制编码 a 97 01100001 b 98 01100010 c 99 01100011
W 0 , W 1 , W 2 , W 3 , W 4 , W 5 , … , W 15 W_0, W_1, W_2, W_3, W_4, W_5, \dotsc, W_{15} W 0 , W 1 , W 2 , W 3 , W 4 , W 5 , … , W 15
W t = σ 1 ( W t − 2 ) + W t − 7 + σ 0 ( W t − 15 ) + W t − 16 W_{t} = \sigma_{1}(W_{t-2}) + W_{t-7} + \sigma_{0}(W_{t-15}) + W_{t-16} W t = σ 1 ( W t − 2 ) + W t − 7 + σ 0 ( W t − 15 ) + W t − 16
其中:
σ 0 = R O T R 7 ( x ) ⊕ R O T R 18 ( x ) ⊕ S H R 3 ( x ) σ 1 = R O T R 17 ( x ) ⊕ R O T R 19 ( x ) ⊕ S H R 10 ( x ) R O T R n ( x ) ≡ x rotated right by n bits S H R n ( x ) ≡ x shifted right by n bits \begin{aligned} \sigma_{0} &= ROTR^{7}(x) \oplus ROTR^{18}(x) \oplus SHR^{3}(x) \\ \sigma_{1} &= ROTR^{17}(x) \oplus ROTR^{19}(x) \oplus SHR^{10}(x) \\ ROTR^n(x) &\equiv x \text{ rotated right by } n \text{ bits} \\ SHR^n(x) &\equiv x \text{ shifted right by } n \text{ bits}\end{aligned} σ 0 σ 1 ROT R n ( x ) S H R n ( x ) = ROT R 7 ( x ) ⊕ ROT R 18 ( x ) ⊕ S H R 3 ( x ) = ROT R 17 ( x ) ⊕ ROT R 19 ( x ) ⊕ S H R 10 ( x ) ≡ x rotated right by n bits ≡ x shifted right by n bits
T 1 ( t ) = h ( t ) + Σ 1 ( e ( t ) ) + C h ( e ( t ) , f ( t ) , g ( t ) ) + K t + W t T 2 ( t ) = Σ 0 ( a ( t ) ) + M a j ( a ( t ) , b ( t ) , c ( t ) ) \begin{aligned} T_1^{(t)} &= h^{(t)} + \Sigma_1(e^{(t)}) + Ch(e^{(t)}, f^{(t)}, g^{(t)}) + K_t + W_t \\ T_2^{(t)} &= \Sigma_0(a^{(t)}) + Maj(a^{(t)}, b^{(t)}, c^{(t)}) \\\end{aligned} T 1 ( t ) T 2 ( t ) = h ( t ) + Σ 1 ( e ( t ) ) + C h ( e ( t ) , f ( t ) , g ( t ) ) + K t + W t = Σ 0 ( a ( t ) ) + M aj ( a ( t ) , b ( t ) , c ( t ) )
其中:
C h ( x , y , z ) = ( x ∧ y ) ⊕ ( ¬ x ∧ z ) M a j ( x , y , z ) = ( x ∧ y ) ⊕ ( x ∧ z ) ⊕ ( y ∧ z ) Σ 0 ( x ) = R O T R 2 ( x ) ⊕ R O T R 13 ( x ) ⊕ R O T R 22 ( x ) Σ 1 ( x ) = R O T R 6 ( x ) ⊕ R O T R 11 ( x ) ⊕ R O T R 25 ( x ) R O T R n ( x ) ≡ x rotated right by n bits S H R n ( x ) ≡ x shifted right by n bits \begin{aligned} Ch(x, y, z) &= (x \land y) \oplus (\neg x \land z) \\ Maj(x, y, z) &= (x \land y) \oplus (x \land z) \oplus (y \land z) \\ \Sigma_0(x) &= ROTR^2(x) \oplus ROTR^{13}(x) \oplus ROTR^{22}(x) \\ \Sigma_1(x) &= ROTR^6(x) \oplus ROTR^{11}(x) \oplus ROTR^{25}(x) \\ ROTR^n(x) &\equiv x \text{ rotated right by } n \text{ bits} \\ SHR^n(x) &\equiv x \text{ shifted right by } n \text{ bits}\end{aligned} C h ( x , y , z ) M aj ( x , y , z ) Σ 0 ( x ) Σ 1 ( x ) ROT R n ( x ) S H R n ( x ) = ( x ∧ y ) ⊕ ( ¬ x ∧ z ) = ( x ∧ y ) ⊕ ( x ∧ z ) ⊕ ( y ∧ z ) = ROT R 2 ( x ) ⊕ ROT R 13 ( x ) ⊕ ROT R 22 ( x ) = ROT R 6 ( x ) ⊕ ROT R 11 ( x ) ⊕ ROT R 25 ( x ) ≡ x rotated right by n bits ≡ x shifted right by n bits
然后更新工作变量:
h ( t + 1 ) = g ( t ) g ( t + 1 ) = f ( t ) f ( t + 1 ) = e ( t ) e ( t + 1 ) = d ( t ) + T 1 ( t ) ( m o d 2 32 ) d ( t + 1 ) = c ( t ) c ( t + 1 ) = b ( t ) b ( t + 1 ) = a ( t ) a ( t + 1 ) = T 1 ( t ) + T 2 ( t ) ( m o d 2 32 ) \begin{aligned} h^{(t+1)} &= g^{(t)} \\ g^{(t+1)} &= f^{(t)} \\ f^{(t+1)} &= e^{(t)} \\ e^{(t+1)} &= d^{(t)} + T_1^{(t)} \pmod{2^{32}} \\ d^{(t+1)} &= c^{(t)} \\ c^{(t+1)} &= b^{(t)} \\ b^{(t+1)} &= a^{(t)} \\ a^{(t+1)} &= T_1^{(t)} + T_2^{(t)} \pmod{2^{32}}\end{aligned} h ( t + 1 ) g ( t + 1 ) f ( t + 1 ) e ( t + 1 ) d ( t + 1 ) c ( t + 1 ) b ( t + 1 ) a ( t + 1 ) = g ( t ) = f ( t ) = e ( t ) = d ( t ) + T 1 ( t ) ( mod 2 32 ) = c ( t ) = b ( t ) = a ( t ) = T 1 ( t ) + T 2 ( t ) ( mod 2 32 )
H 0 ′ = H 0 + a ( 64 ) ( m o d 2 32 ) H 1 ′ = H 1 + b ( 64 ) ( m o d 2 32 ) H 2 ′ = H 2 + c ( 64 ) ( m o d 2 32 ) H 3 ′ = H 3 + d ( 64 ) ( m o d 2 32 ) H 4 ′ = H 4 + e ( 64 ) ( m o d 2 32 ) H 5 ′ = H 5 + f ( 64 ) ( m o d 2 32 ) H 6 ′ = H 6 + g ( 64 ) ( m o d 2 32 ) H 7 ′ = H 7 + h ( 64 ) ( m o d 2 32 ) \begin{aligned} H_0' &= H_0 + a^{(64)} \pmod{2^{32}} \\ H_1' &= H_1 + b^{(64)} \pmod{2^{32}} \\ H_2' &= H_2 + c^{(64)} \pmod{2^{32}} \\ H_3' &= H_3 + d^{(64)} \pmod{2^{32}} \\ H_4' &= H_4 + e^{(64)} \pmod{2^{32}} \\ H_5' &= H_5 + f^{(64)} \pmod{2^{32}} \\ H_6' &= H_6 + g^{(64)} \pmod{2^{32}} \\ H_7' &= H_7 + h^{(64)} \pmod{2^{32}}\end{aligned}
H 0 ′ H 1 ′ H 2 ′ H 3 ′ H 4 ′ H 5 ′ H 6 ′ H 7 ′ = H 0 + a ( 64 ) ( mod 2 32 ) = H 1 + b ( 64 ) ( mod 2 32 ) = H 2 + c ( 64 ) ( mod 2 32 ) = H 3 + d ( 64 ) ( mod 2 32 ) = H 4 + e ( 64 ) ( mod 2 32 ) = H 5 + f ( 64 ) ( mod 2 32 ) = H 6 + g ( 64 ) ( mod 2 32 ) = H 7 + h ( 64 ) ( mod 2 32 )
将 H i ′ H_i' H i ′ 依次拼接起来就得到了我们梦寐以求的 Hash 值!
a ( 0 ) = H 0 b ( 0 ) = H 1 c ( 0 ) = H 2 d ( 0 ) = H 3 e ( 0 ) = H 4 f ( 0 ) = H 5 g ( 0 ) = H 6 h ( 0 ) = H 7 \begin{aligned} a^{(0)} &= H_0 \\ b^{(0)} &= H_1 \\ c^{(0)} &= H_2 \\ d^{(0)} &= H_3 \\ e^{(0)} &= H_4 \\ f^{(0)} &= H_5 \\ g^{(0)} &= H_6 \\ h^{(0)} &= H_7\end{aligned} a ( 0 ) b ( 0 ) c ( 0 ) d ( 0 ) e ( 0 ) f ( 0 ) g ( 0 ) h ( 0 ) = H 0 = H 1 = H 2 = H 3 = H 4 = H 5 = H 6 = H 7